Gravity

You and I are solid objects that live in a space-time world. We move through a field of space using co-ordinates (x, y, and z) at time (t) to locate our position in a forward moving direction. Time (t) is really a marker as we can’t travel through time nor can we change it in any way except by altering the time we do something. For instance, you and I can meet at a restaurant in the middle of the country whose co-ordinates are (x, y, z) at time (t). There are also other people in the restaurant at time (t) at internal restaurant co-ordinates (x, y, and z). To state the obvious, they cannot stand on exactly the same spot we are standing on because only one solid object can be standing on one (x, y, and z) co-ordinate at the same time (t) with a gravity value (g). In simple terms gravity (g) is normal space energy but doesn’t become apparent to us until a depression caused by an object at some location (x, y and z) in our field of space (s) at time (t).  A favourite example is a large mass (m) like the earth which is located at some location (x, y, and z) in our universe at time (t). In other words a mass (earth) flexes the energy in our space (field) at time (t) or at some space-time which creates a force (g). We call this force gravity (g). The quantum world is the reverse of the real world. Space only exists as a marker in the quantum world similar to time in our real world. Since these bundles of energy can travel in multiple directions through time as a quantum wave (w) they can appear at several quantum (x, y and z) locations which function as markers in the quantum world. This is possible because time (t) has only a past, present or future without a definite corresponding space (s) location. The quantum energy field also exists which has its’ own quantum gravity value (g) associated with that particular quantum energy particle.  Quantum objects travel as waves through time. It all comes down to the old tree and forest conundrum. We have compared gravity in different locations (x, y, and z) at different times (t) in our real and quantum worlds. You have seen that both are equivalent, yet different, because our real world is primarily location based (x, y, and z) at different times (t) whereas our quantum world is time based (t) at different locations (x, y and z). Therefore we have the same, yet different trees depending on their locations, time and function  in the real and quantum world and the forest is the same in function and principle depending on its’ location, time and function in the real and quantum worlds. When we look at the quantum world from our space- time world an automatic conversion must occur to something we can understand and interpret in our space-time world. Since only one solid object can exist at location (x, y, and z) at time (t) with a gravity value (g) in our space-time world the choice is either the quantum energy bundle (particle) or its’ corresponding energy wave.

Therefore:

1.       Both real world and quantum worlds have gravity fields.

2.       Both real world and quantum world objects / energy packets have gravity.

3.       Both real world and quantum world locations / time have gravity.

The Reimann Hypothesis Imaginary Math

The Riemann zeta function states all non-trivial zeros have a real part equal to ( ½ ) . When you think about it, this statement is rather profound . In our real world mathematics a zero is either a placeholder in a number ( 301 ) or has a value of zero ( 0 ) . Riemann didn't say so but as soon as these zeros ( 0 ) crossed the line ( y = ½ ) that zero had a value of ( ½ ) . Riemann went on to extend the original equation into the imaginary plane and that meant that zero ( 0 ) had a value of ( ½ + it ) on the line ( y = ½ + it ) where.”i” is imaginary and “t” is real . Riemann's unspoken thought suggests that there is undiscovered mathematics .

When you think about this statement zero can have a value of :

1. zero ( 0 )
2. ½
3. ( ½ + it )

Riemann took the original equation into the complex plane which is represented by “i” . Since zero is a single digit, the undiscovered mathematics seems to indicate that if the digits in a number are added they can be placed on a line that has a single value. Since Riemann took the original equation into the complex plane, this means that zero ( 0 ) can have a single value that is part real and part imaginary . For instance if the digits in the number ( 47 ) are added ( 4 + 7 = 11 ) and ( 1 + 1= 2 ) , then ( 47 ) is on the line ( y = 2 ) . ( 47 ) can also be on the line ( y = 11 ) because ( 4 + 7 = 11 ) . Zero ( 0 ) doesn't have a “real” digit so it can't be on a line that has a “real” meaning ( y = 0 ) . Zero ( 0 ) in the numerical system seems to be equivalent to “i” in the symbolic mathematical system, except that zero can have any value whereas “i” is limited to √ - 1 . The Riemann Hypothesis has something to do with primes . A prime is a number that can only be divided evenly by itself and one ( 1 ) . A prime number has the digits ( 1, 3, 7, 9 ) in column ( 0 ) which is the far right column . The single digit primes are ( 1, 2, 3, 5, 7 ) . Primes with more than one digit are on the lines ( 1, 2, 4, 5, 7, 8 ) . The number of primes are infinite . The ordinary numbers that aren't primes are also infinite .That being said, Riemann developed a formula for the number of primes less than a number . The “number” was defined as the sum of the zeros ( 0 ) in the zeta function. Riemann had taken the original equation into the complex plane which meant that the value of the zero ( 0 ) was now ( ½ + it ) on the line ( y = ½ + it ) . The formula said that the magnitude of the oscillations of the primes around their expected position is controlled by the real parts of the zeta function . If the zeros are on the line ( y = ½ + it ) , their value is ( ½ + it ) which means ( it ) has to have a “real” value. If ( it ) is real you add up the numbers obtaining a real number . Lastly , the error term in the prime number theorem is closely related to the position of the zeros . When you think about the statement “ the “number” was defined as the sum of the zeros ( 0 ) on the zeta function “ it really doesn't matter because the number of primes are always less than any other number. The first prime numbers are ( 1, 2, 3 ) . Their positions are ( 1, 2, 3 ) . The error term in the prime number theorem is closely related to the position of the zeros . If you multiply the primes ( 1, 2, 3 ) by 100% you get the prime's positions ( 1, 2, 3 ) . If you multiply the primes ( 1, 2, 3 ) by 10% you obtain ( .1, .2, .3 ) for the position of the primes . You dropped one ( 1 ) zero and your calculation was out. Therefore the error term in the prime number theorem is closely related to the position of the zeros. The single digit primes are ( 1, 2, 3, 5, 7 ) . Prime number 5 is in the fourth ( 4^th ) position . If you multiply prime 5 by .8 you get 4 . The number ( .8 ) is obtained by adding using the zeta function . Prime number 7 is in the fifth position ( 5^th ) . If you multiply 7 X .714285714 you get 5. This term is obtained by adding the zeta function . If you add zeros to .714285714 or put zeros somewhere within .714285714 ( for instance .7140285714 ) you will soon see that the error term in the prime number theorem is closely related to the position of the zeros .

Our Real World & The Quantum World Compared

Space and Time exist in our real world as well as in the quantum world . Space in our real world has ( x, y, z ) dimensions. Time in the quantum world has past , present, future . Time in our real world is used as a marker representing the past, present and future but you can't physically travel through or along it in all directions . Velocity or speed measures distance or space traveled in units of time which are essentially a marker , marking out distance. Acceleration or increase in speed measures increasing distance or space in units of time which are essentially a marker, marking out increases in distance traveled . Space in the quantum world is used as a marker in all directions but you can't literally travel through it . Gravity in our real world is used to anchor things in space by bending strings of space. Strings of space are usually bent around masses such as the earth, thereby creating gravity which we see as weight. Gravity in the quantum world is essentially past, present and future time anchored in one place because travel through space doesn't exist . Since travel through space doesn't exist in the quantum world, travel is managed by the processes of entanglement, superlocation, and superposition. Superposition shows all the states, possibilities and information at the same time in the past, present and future in the same location. Superlocation means that the past, present and future can exist at the same physical location because travel through physical space doesn't exist in the quantum world. Since travel through physical space doesn't physically exist in the quantum world more than one thing can exist at the same spot or location in the past, present and future. This is quantum gravity as it relates to quantum time . In other words, this means that the past, present and future all co-exist at the same time at the same spot or location in the quantum world. The existence of superlocation and superposition means that everything that is knowledge ( states, possibilities and information ) exists at one superlocation all at once in the past, present and future. Travel in the quantum world is done through a process called entanglement, because the quantum world can't move through physical space because travel through physical space doesn't exist . If I have a past, present and future quantum particle here and another past, present and future quantum particle over there, I can entangle my past, present, future quantum particle with the other past, present, future quantum particle to make both particles have the same states, possibilities, and information at the same time in the same past, present, future. This process of entanglement of two quantum particles also involves quantum time acting relativistically in the past, present and future. Time from a relativistic viewpoint means that if I do something in the quantum world, I also do it in the present, past and future at the same time because travel through physical space doesn't exist. Paradoxically, if someone comes along and chooses my quantum past, my quantum past becomes his / her quantum present because he / she chose it in his / her quantum present. This also means that he / she can relativistically travel through quantum relativistic time into someone else's past and future. If he / she altered my quantum past / present / future, his / her quantum past / present / future would also be altered because he / she and I are relativistically linked in relativistic time. This means that someone cannot realistically travel through relativistic quantum time to destroy his / her grandfather without wiping out his / her relativistic existence. The final mind blower is that someone's quantum present can alter my quantum past so in essence someone's present “cause” interrupted my past effect, which means that in the quantum world effect can precede cause.    

The Weird Riemann Hypothesis

Sometimes in life, you stumble across something that holds more meaning than first meets the eye. Meeting your future husband or wife for the first time and not realizing it is a good example. Mathematically, Dirac's equation is probably the most famous something. Dirac had the ability to visualize an equation in terms of geometry . Dirac came up with an equation that was more insightful than he first realized which you can look up in the Internet . Riemann's something was when it was realized that his zeta function said that the magnitude of the oscillations of primes around their expected position is controlled by the real parts of the zeros of the zeta function . You and I can read the words but what is the meaning without repeating the sentence as an answer ????

Numbers basically break down into the following three areas:

1. Rational
2. Imaginary
3. Irrational
   Rational Numbers have a beginning and an end. Examples of rational numbers are ( 1, 2, 3, 4 ) . Imaginary numbers are numbers such as the square root of ( - 1 ) ( √ -1 ) . Irrational numbers have a beginning but no end, and seem to go on forever. Examples of Irrational numbers are Pi, “e” or Euler's number . It suddenly occurred to me that when it was realized that Riemann's zeta function said that the magnitude of the oscillations of primes around their expected position is controlled by the real parts of the zeros they were really talking about irrational numbers except that these irrational numbers were governed by zeros in the digits of the number . If you put all the prime numbers on a straight line and numbered them, you'd know their location on that straight line . Of course this is impossible . If Riemann's zeta function said that the magnitude of the oscillations of primes around their expected position is controlled by the real parts of the zeros there is an implication that an irrational number controlled by the placement of zeros ( 0 ) in the digits when multiplied by the prime number would indicate the true position of the prime on that line and by extension all the primes that preceded it . If you multiply a number by an irrational number that has a beginning and no end you will soon see that you get different answers. Riemann also said that all his non-trivial zeros had a value of ( ½ ) which seems odd when you think about it . How can a zero have the value of ( ½ ) ???? Exercising our imagination, which seems to be as temporarily irrational as is our theme, it seems that every time a zero is on Riemann's line ( y = ½ ), it has the value of ½ . If you are also looking for a major brain freeze, you can also say that if all the primes are placed on the line ( y = ½ ) from 1 to infinity they also have the value of ( ½ ) . Weird as it may seem, we are busy finding non-trivial zeros on the line ( y = ½ ) that have a value of ( ½ ) because they are on the line ( y = ½ ) . Consequently, we now have primes and zeros on the line ( y = ½ ) which all have the value of ( y = ½ ) because they are on the line ( y = ½ ) . A prime is a number that can only be divided by itself and one ( 1 ). The position of the primes from ( 1 to 31 ) can be calculated by multiplying the primes ( 1 to 31 ) by ( .509999999 ^ 1). From ( 37 to 97 ) the primes can be multiplied by ( .509999999 ^ 2 ) to keep the calculated distance close to the actual distance. This is how it works in principle by manipulating zeros ( 0 ) and the addition or subtraction of two irrational numbers Pi and “e” .

For Every Zero Crossing Riemann's Line ( y = ½ )

Sometimes in life, you stumble across something that holds more meaning than first meets the eye. Meeting your future husband or wife for the first time and not realizing it is a good example. Mathematically, Dirac's equation is probably the most famous something. Dirac had the ability to visualize an equation in terms of geometry . Dirac came up with an equation that was more insightful than he first realized which you can look up in the Internet . Riemann's something was when it was realized that his zeta function said that the magnitude of the oscillations of primes around their expected position is controlled by the real parts of the zeros of the zeta function . You and I can read the words but what is the meaning without repeating the sentence as an answer ????  

Mathematics basically breaks down into the following three areas:

1. Numbers.
2. Symbols.
3. Lengths
   Numbers can represent anything. Symbols such as x or y are usually equal to something which is up to you to discover. These symbols may be in a formula expressing relationships which are familiar to anyone that has ever studied algebra. These relationships in algebra are generally a static value as only one numerical answer is needed. Lengths are usually the distance from the beginning of something. An example of this concept is the measurement of a board before you cut it with a saw. The Riemann Hypothesis also hints at the concept of length as it relates to the number of primes. A prime is a number that can only be divided evenly by itself and one ( 1 ) . The five ( 5 ) single digit prime numbers are ( 1. 2, 3, 5, 7 ) . Riemann came up with the formula ( s = ½ + it ) that related to another formula. Without filling in the background, the Riemann Hypothesis implies that if the zeros consistently cross the line ( y = ½ ) in relation to the formula ( s = ½ + it ) then these zeros have something to do with the distribution of primes. There is an implicit idea here that every crossing of a zero on the line ( y = ½ ) is related to the position of a corresponding prime from the beginning of the line ( y = ½ ) to the end of the line ( y= ½ ) at infinity. Theoretically, if the values of Riemann's formula were chosen correctly, the calculation of the zeros crossing the line would give you the distance of a known prime from the beginning of ( y = ½ ) . This means that if the location of the zero crossing the line ( y = ½ ) were accurate that location would correspond with the position of a prime on the line ( y = ½ ) . Riemann's formula is really a disguised calculus problem using zeros ( 0 ) to adjust the placement of a prime on the line ( y = ½ ) . In other words, if you adjust the zero in a mathematical expression how close can you get the relevant known prime to its' actual position on the line ( y = ½ ) ???? This position calculation would give you the number of primes from the beginning of the line ( y = ½ ) . My previous blogs on this topic will give you an idea as to how the calculation is done. Calculus, using symbols, is the study of the change in the length of a formula containing symbols that change in length. One of these symbols is ( c ) which represents a constant ( whole number ) which never changes. The accepted length of a constant ( c ) in calculus ( d (c)) is zero ( 0 ) but that isn't correct because Riemann's intuition told him that the zeros which are also a constant had a real value of ( ½ ) on his line ( y = ½ ) consisting of primes. The actual length of any ordinary constant is the sum of its' digits. 47 would have a length of 11 or 2 ( 4 + 7 = 11 ) or ( 1 + 1 = 2 ). 

The Riemann Hypothesis Solved Using Calculus Limits

Mathematics basically breaks down into the following three concepts:

1. Numbers.
2. Symbols.
3. Lengths
   The symbols such as x or y are usually equal to something which is up to you to discover. These symbols may be in a formula expressing relationships which are familiar to anyone that has ever studied algebra. These relationships in algebra are generally a static value as only one numerical answer is needed. Calculus was the next major step. Calculus is the study of limits which involve fractions. Limits are concerned with how close you can get to something I call a brick wall ( limit ) without actually touching it. How close is actually the calculation of length before you hit the wall or limit. Here you are dealing with fractions. Calculus, using symbols, is the study of the change in the length of a formula containing symbols that change in length. If you have symbols in a formula, what happens to the formula when that symbol or symbols change in length ???? To make life simpler, the initial formula is simplified to lessen the potential confusion. In any language, as in mathematics, there are many ways to express an idea .
   Riemann expressed his idea using the following formulas:

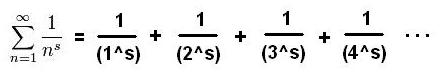
Riemann said that the “s” in the above equation was ( s = ½ + it ). The “i” in it represented an imaginary number and the “t” represented a real number. He also said that all his non – trivial zeros lie on the line ( y = ½ ) . Innumerable calculations up to the present time have proven that Riemann's conjecture is true but there also may be an exception yet to be discovered. The Riemann Hypothesis also implies that if the zeros consistently cross the line ( y = ½ ) then these zeros have something to do with the distribution of primes. There is an implicit idea here that every crossing of zeros on the line ( y = ½ ) is related to the position of a relative prime beginning at the beginning of the line ( y = ½ ) and the end of the line ( y= ½ ) at infinity. Theoretically, if the values of Riemann's formula were chosen correctly the

calculation of the zeros crossing the line in terms of distance of an unknown prime from the beginning of ( y = ½ ) would be accurate. The only variable in the equation is in the one ( s = ½ + it ) or ( it ). Riemann's formula is really a disguised calculus problem using zeros ( 0 ) to adjust the placement of a prime on the line ( y = ½ ) . In other words, if you adjust the zero in a mathematical expression how close can you get the relevant unknown prime to its' actual position on the line ( y = ½ ) ???? The Riemann function backs up this concept by saying that the magnitude of the oscillations of primes around their expected position is controlled by the real parts of the zeros of the zeta function. In particular the amount of error is closely related to the position of the zeros . This means that the unknown value of ( it ) has adjustable zeros as well as a real number which is used to fine tune the position or location of a particular prime on the line ( y = ½ ) . Primes are numbers that can only be divided evenly by themselves and one ( 1 ). The single digit prime numbers are 1, 2, 3, 5, 7 . If you draw a straight line and put some or all the primes on it, you will soon see that there isn't a standard distance between the primes. You can also count the primes from the beginning of the line but there isn't any way of accurately saying how many primes precede a prime without counting all the primes from the beginning up to that particular prime. Let's assume that the non-trivial zeros lie on the line ( y = ½ ) . For the sake of convenience we can also put all the primes from one ( 1 ) to infinity on the line ( y = ½ ) and indicate their position on the line ( y = ½ ) from the beginning of the line ( y = ½ ) . The single digit primes are five ( 5 ) in number consisting of 1, 2, 3,. 5, 7. If you arbitrarily multiply the primes by ( ½ ) you will soon see that your answer has usually very little relationship to the primes true position on the line ( y = ½ ) . In other words, by multiplying by ( ½ ) you will soon see that if all the numbers are written down from zero ( 0 ) to infinity that ( ½ ) of them aren't primes. The Riemann Hypothesis also implies that if the zeros consistently cross the line ( y = ½ ) then these zeros have something to do with the distribution of primes. If the zeros consistently cross the line ( y = ½ ) than these zeros ( 0 ) can be used in the calculation . We now have the value of the line ( ½ ) plus the zeros to use in some way to see if we can calculate the position of the primes on the line ( y = ½ ) from the beginning. Multiplying by ( ½ ) or ( .5 ) or ( .50 ) doesn't change your original answer. Using ( .05 ) also doesn't improve things to any great extent. Riemann also said that the zeros can be manipulated ( positions changed or zeros added ) in order to get the primes closer to their true location. This manipulation changes the physical distance between the primes. To accomplish this manipulation, place some digits after the zero ( 0 ) in ( .50 ) such as forming ( .509999 ) . Therefore:

1. 5 X ( .509999 ) = 2.549995 (4)
2. 7 X ( .509999 ) = 3.569993 ( 5 )

3. 11 X ( .509999 ) = 5.609989 ( 6 )

This basic principle calculates the position of the primes fairly accurately up to prime 31.

Using the same multipliers on the next prime ( 37 ) we get ( 37 X .509999 = 18.869963. Prime ( 37 ) is actually the 13^th prime. Riemann said that the zeros can be manipulated ( positions changed or zeros added ). We still need the ( ½ ) in Riemann's line ( y = ½ ) and the ( 9's ). If we take ( .509999 ) and multiply it by itself ( ( .509999 X .509999 = .26009898 ).

1. ( 37 X .509999 X ,509999 = 9.62366226 ( 13 )

This calculation shows that the calculated position is short of the true position by about ( 13 – 9.62366226 = 3.37633774 ). The difference is approximately equal to Pi ( 3.141592654 ). In some calculations the difference is about the natural number ( e ) ( 2.71828`828 ).

In summary, Riemann's intuition told him that the zeros had a real value of ( ½ ) which was true since the digit ( ½ ) is used in the calculation. Riemann's intuition also told him that the zeros can be manipulated ( position changed or zeros added ) which is also true. This manipulation of zeros ( 0 ) is really using the principles of limits in calculus to see how close you can find a factor when multiplied by a prime that will give you the position of that prime on the line ( y = ½ ). What Riemann missed was that the calculation involved the number 9 and that Pi ( 3.141592654 ) and the natural number ( e ) ( 2.718281828 ) might have to be added or subtracted from the final answer. Riemann also missed that powers would also have to be used.

In general for calculating the location of any prime you:

1. Count the number of digits in a prime number. For instance 7919 has 4 digits. Subtract 1 from the number of digits ( 4 - 1 = 3 ) for 7919. Form another number equal to the number of digits in 7919 ( 4 ) by putting ( .5 ) in the far left column and 9 in the far right column. ( .5—9 ). Fill the middle with Riemann Hypothesis zeros ( 0 ) forming a four digit number ( .5009 ). Raise ( .5009 ) to the power of 3 ( which is the number of digits in 7919 ( 4 ) minus 1 ( 4 - 1 = 3 ). ( .5009 ) ^ 3 = .125676215. Multiply 7919 X .125676215 which equals 995.2299524. 7919 is the 1000^th prime. The answer is out by approximately 5. Adjust the error by adding or subtracting Pi or (e).

The Clay Mathematics Institute is offering a $1,000,000 prize for the solution to the Riemann Hypothesis. From my reading, it seems to involve proving whether or not all the zeros lie on the line ( y = ½ ) . Since I have shown how the Riemann Hypothesis relates to the location of the primes and by extension how many primes precede that prime ( counting 1, 2, 3, 4 ), it seems to me it is largely academic as to whether all the zeros lie on the line ( y = ½ ) . I've also proved that the manipulation of the zeros as implied by Riemann can bring a prime closer to its' position using the principles of Calculus.

The Universe & The Heisenberg Principle

I got to thinking about the universe and Heisenberg . If I mentioned the number 56, all you know is that it is the number 56.

The number 56 could be anything but to keep it simple we'll keep it to these three possibilities:

1. A particle which has weight or mass.
2. 
   
   A length.
3. 
   
   A change in the length.
   
   
   Einstein said that mass and energy are equivalent. This means that 56 under ( 1 ) has both a mass and energy of 56. In our real world, we have physical space and time or in other words Einstein's space-time. Somewhere in our real world we have the number ( 56 ) at Einstein's space location ( x, y, z ) at Einstein's time ( t ). Time in Einstein's space-time world is only a marker. If we ran across a particle in our space-time world at location ( x, y, z ) at marker time ( t ) we could measure its' mass or weight. The particle could be lying still, moving at a constant velocity or accelerating. If the particle was lying still we could easily measure its' mass or weight. If the particle was moving at a constant velocity or under acceleration, we would have to stop it and measure its' mass or weight. Our stopping of the particle means that its' velocity or acceleration are lost to measurement. If the particle had a velocity or was under acceleration, we could measure the velocity or acceleration while the particle was under velocity or acceleration but we wouldn't have a clue about the particle's mass or weight. Heisenberg said we could measure mass or weight but not velocity or acceleration at the same time. This means we are certain about one ( ( mass or weight ) ) but uncertain about the other ( velocity or acceleration ). The unknown particle could have a velocity of 56 ( 2 – constant length / unit time ) or an acceleration of 56 ( 3 – change in length traveled / unit time ). The quantum world is the reverse of the real world. Space only exists as a marker in the quantum world. In the quantum world we think of space as right here or over there. We can't travel through space in the quantum world to get from here to there because travel through space doesn't physically exist in the quantum world. The quantum world is made up of energy-time. Their literally aren't any particles in the quantum world. What we see as particles in the space-time world are clouds in the quantum world. These concentrations of clouds can be treated as particles in the quantum world. These concentrations of clouds may or may not have mass. They may also spin up, down or at an angle. These clouds may be still at the center, yet spin on the periphery or not spin on the periphery . Sometimes the spin drags the interior part of the cloud in a circle so it rotates at different speeds returning to its' original orientation at different times. We call this phenomena different ( return to normal ) rotations ( ie: 2 ½ X ). Sometimes the entire cloud consistently spins so the rotation for everything in the cloud is consistent ( one ( 1 ) rotation ). Energy in the energy-time quantum world can travel anywhere so the concentrations of energy aren't even but are on average statistically even. Quantum time in the quantum world can be sliced into smaller and smaller parts. Since energy in the quantum world isn't distributed evenly sometimes more energy ends up in a sliced piece of quantum time than is statistically expected.
   The universe is made up of the following three layers.
   1. Einstein's space-time world or our real world.
   2. 
    The dark energy- dark matter layer.
   3. 
   Q The quantum world.

Time in our space-time world moves all of us outward in a forward direction. That is why we age, things deteriorate and require repair or replacement. Our space-time world sits on a world of dark matter and dark energy. This dark energy and dark matter both expands and accelerates the expansion of our universe resulting in things in our universe becoming further apart. Dark matter and dark energy are the left over debris from antimatter matter interactions.

The quantum world exists underneath the dark energy and dark matter layer. When quantum time is sliced into smaller and smaller pieces it also compresses quantum energy which may be in greater volume in that slice of time then statistically normal. If that happens we know how much we sliced time, but we don't know how much energy that slice of time contains. The energy in that slice of time, if large enough, may or may not form a particle. If the particle is formed it goes up through the dark matter and dark energy layer causing an equivalent antimatter particle to be produced. These particles annihilate themselves in our space-time world and the respective energies return to the dark matter and dark energy layer as well as to the quantum layer. This action - reaction in the quantum layer creates quantum foam or quantum fluctuation which is basically the wave action of the returning quantum energy which is equivalent to the previously produced particle . Quantum mechanics is concerned with this phenomena. If the matter – antimatter process is quick enough and the energy returned fast enough to the quantum world nothing is noticed in our real world of space-time. Space, energy and time in our real world appear to be three separate things but in the energy-time or quantum world they are all the same thing viewed differently.